机器学习致力于研究如何通过计算的手段，利用经验来改善系统自身的性能。在计算机系统中，“经验”通常以“数据”的形式存在，因此，机器学习所研究的主要内容，是关于在计算机上从数据中产生的“模型”的算法，即“学习算法”。有了学习算法，我们就把经验数据提供给它，它就能基于这些数据产生模型，在面对新的情况时，模型会给我们提供相应的判断。

主要任务：
分类：根据每个实体的特征进行不同种类的区分。

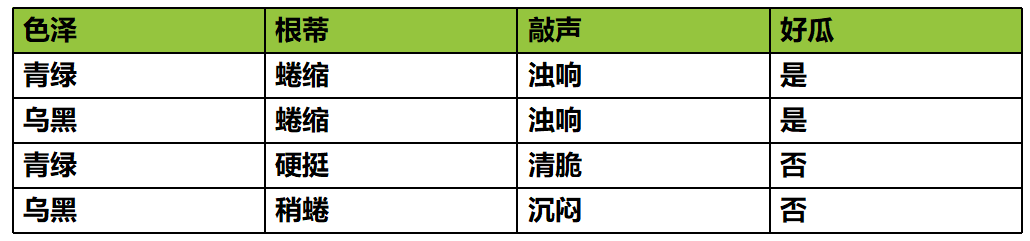
回归：回归任务的目标是预测一个连续值，编程术语叫作浮点数。

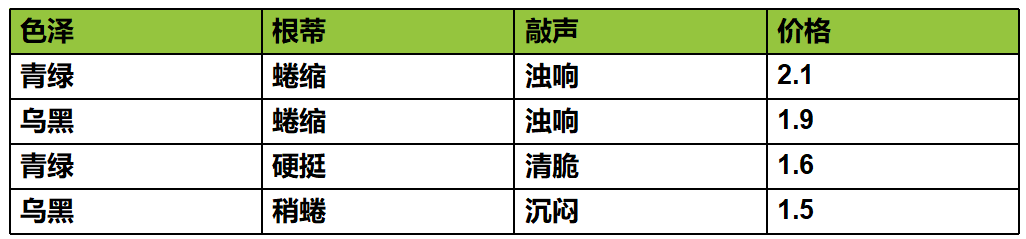
聚类：聚类属于无监督学习，它是指我们的数据只有输入，没有输出，并需要从这些数据中提取知识。

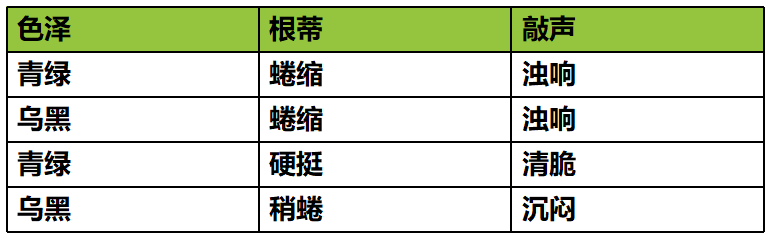
分类和回归属于监督学习，这类算法必须知道预测什么，即目标变量的分类信息。与监督学习相对应的是无监督学习，此时数据没有类别信息，也不会给定目标值。半监督学习用未标记的数据帮助少量有标记的数据进行模型训练。

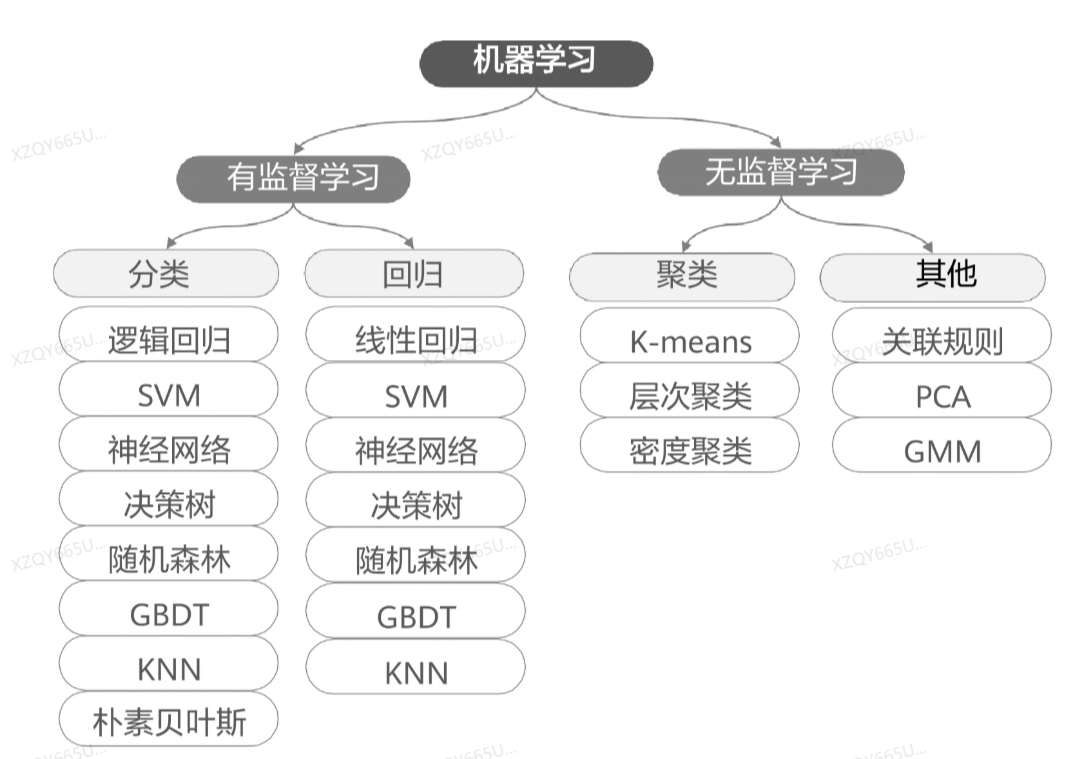
常见术语

• 我们把数据中的每一行称为一个示例或样本；

• 反映事件或对象在某方面的表现或性质的事项，如：色泽、根蒂、敲声，称为属性或特征；

• 属性上的取值，例如：青绿、乌黑。称为属性值或特征值；

• 我们把一个示例（样本）称为一个特征向量。

• 从数据中学得模型的过程称为“学习”或“训练”，这个过程通过执行某个学习算法来完成。训练过程中使用的数据称为“训练数据”，其中每个样本称为一个“训练样本”，训练样本组成的集合称为“训练集”，学习过程就是为了找出或逼近真相。

k邻近算法（knn）

from sklearn.neighbors import KNeighborsClassifier
所谓 K 最近邻，就是 k 个最近的邻居的意思，说的是每个样本都可以用它最接近的 k 个邻居来代表。
在 sklearn 中通过 KNeighborsClassifier 方法实现 knn ， KNeighborsClassifier 的构造函数中有一个常用的参数可以设置：
n_neighbors：n_neighbors=n 表示样本与最近的 n 个样本进行比较， n_neighbors 的值默认为 5。
KNeighborsClassifier 类中的 fit 函数用于训练模型，fit 函数有两个向量输入：
X：大小为 [ 样本数量,特征数量 ] 的 ndarray，存放训练样本；
Y：值为整型，大小为 [ 样本数量 ] 的 ndarray，存放训练样本的标签值。
KNeighborsClassifier 类中的 predict 函数用于预测，返回预测值， predict 函数有一个向量输入：
X：大小为 [ 样本数量,特征数量 ] 的 ndarray，存放预测样本。

线性回归

from sklearn.linear_model import LinearRegression
在 sklearn 中通过 LinearRegression 方法实现线性回归。
fit函数和predict函数的使用方式同上。

图像分割

图像的基础操作
导入模块
from PIL import Image

# 打开图像文件
im = Image.open("example.jpg")
# 将im转换成ndarray
img = np.array(im)# 转换成heightU*width*channels的三维数组
# 改变数组的形状
np.reshape(array, newshape, order='C')
img.reshape(-1,3)# -1表示自适应
# 缩放到指定尺寸
resized_image = image.resize((200, 200))
# 显示图像
image.show()
# 获取图像信息
print(image.format)  # 图像格式 (如 JPEG, PNG)
print(image.size)    # 图像尺寸 (宽度, 高度)
print(image.mode)    # 图像模式 (如 RGB, L 表示灰度)

对图片的不同区全域进行聚类
GaussianMixture 是 sklearn 提供的高斯混合聚类的一个类，该类的构造函数中可以根据实际需要设置很多参数。但常用的参数是 n_components 和 max_iter。其中：
n_components ：想要聚成几个簇，类型为 int；
max_iter ：迭代次数，类型为 int。
fit函数和predict函数的使用方式同上。
效果：

（a）原图

（b）分割图像

逻辑回归

逻辑回归（Logistic Regression）是一种用于解决分类问题的统计模型，尤其适用于二分类问题。它的核心思想是通过一个线性组合的特征来预测样本属于某个类别的概率，并使用 sigmoid 函数 将线性组合的结果映射到 [0, 1] 区间，表示概率值。
在 sklearn 中，使用 LogisticRegression 方法实现逻辑回归算法， LogisticRegression 的构造函数中有三个常用的参数可以设置：

solver：{'newton-cg','lbfgs','liblinear','sag','saga'} ，分别为几种优化算法。默认为 liblinear 。

C：正则化系数的倒数，默认为 1.0，越小代表正则化越强。

max_iter：最大训练轮数，默认为 100。
fit函数和predict函数的使用方式同上。
逻辑回归（Logistic Regression）是一种用于解决分类问题的统计模型，尤其适用于二分类问题。它的核心思想是通过一个线性组合的特征来预测样本属于某个类别的概率，并使用 sigmoid 函数 将线性组合的结果映射到 [0, 1] 区间，表示概率值。

逻辑回归的数学模型

1. 线性组合

逻辑回归首先对输入特征进行线性组合：

z = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \dots + \beta_n x_n

2. Sigmoid 函数

将线性组合的结果 ( z ) 通过 sigmoid 函数（也称为逻辑函数）映射到 [0, 1] 区间：

sigma(z) = \frac{1}{1 + e^{-z}}

sigmoid 函数的输出可以解释为样本属于正类（类别 1）的概率：

P(y=1 | x) = \sigma(z) = \frac{1}{1 + e^{-(\beta_0 + \beta_1 x_1 + \beta_2 x_2 + \dots + \beta_n x_n)}}

3. 分类决策

根据概率值进行分类决策：

• 如果 ( P(y=1 | x) > 0.5 )，则预测样本属于正类（类别 1）。
• 如果 ( P(y=1 | x) < 0.5 )，则预测样本属于负类（类别 0）。

损失函数

逻辑回归使用 对数损失函数（Log Loss）来衡量模型预测的概率分布与真实标签之间的差异。对于二分类问题，损失函数定义为：

J(\beta) = -\frac{1}{m} \sum_{i=1}^m \left[ y^{(i)} \log(P(y^{(i)}=1 | x^{(i)})) + (1 - y^{(i)}) \log(1 - P(y^{(i)}=1 | x^{(i)})) \right]

其中：

• ( m ) 是样本数量。
• ( y^i ) 是第 ( i ) 个样本的真实标签（0 或 1）。

参数估计

逻辑回归通过最大似然估计（Maximum Likelihood Estimation, MLE）来估计模型参数。具体来说，最大化对数似然函数：

\ell(\beta) = \sum_{i=1}^m \left[ y^{(i)} \log(P(y^{(i)}=1 | x^{(i)})) + (1 - y^{(i)}) \log(1 - P(y^{(i)}=1 | x^{(i)})) \right]

在实际应用中，通常使用梯度下降法或其他优化算法来最小化损失函数 ( J(β) )。

正则化

为了防止过拟合，逻辑回归可以加入正则化项。常见的正则化方法包括：

1. L1 正则化：

   J(\beta) = -\frac{1}{m} \sum_{i=1}^m \left[ y^{(i)} \log(P(y^{(i)}=1 | x^{(i)})) + (1 - y^{(i)}) \log(1 - P(y^{(i)}=1 | x^{(i)})) \right] + \lambda \sum_{j=1}^n |\beta_j|

2. L2 正则化：

   J(\beta) = -\frac{1}{m} \sum_{i=1}^m \left[ y^{(i)} \log(P(y^{(i)}=1 | x^{(i)})) + (1 - y^{(i)}) \log(1 - P(y^{(i)}=1 | x^{(i)})) \right] + \lambda \sum_{j=1}^n \beta_j^2

   其中：

• λ是正则化系数，控制正则化的强度。

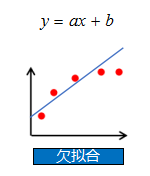
• 正则化强度越大（λ 越大），模型会更简单，倾向于欠拟合。

• 正则化强度越小（λ 越小），模型会更复杂，倾向于过拟合。